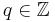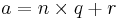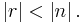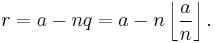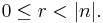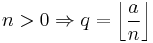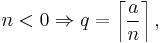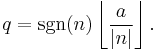Modulo operation

In computing, the modulo operation finds the remainder of division of one number by another.

Given two positive numbers, $a$ (the dividend) and $n$ (the divisor), a modulo n (abbreviated as a mod n) can be thought of as the remainder, on division of a by n. For instance, the expression "5 mod 4" would evaluate to 1 because 5 divided by 4 leaves a remainder of 1, while "9 mod 3" would evaluate to 0 because the division of 9 by 3 leaves a remainder of 0; there is nothing to subtract from 9 after multiplying 3 times 3. (Notice that doing the division with a calculator won't show you the result referred to here by this operation, the quotient will be expressed as a decimal.) When either $a$ or $n$ is negative, this naive definition breaks down and programming languages differ in how these values are defined. Although typically performed with a and n both being integers, many computing systems allow other types of numeric operands. The range of numbers for an integer modulo of n is 0 to n - 1. (n mod 1 is always 0; n mod 0 is undefined, possibly resulting in a "Division by zero" error in computer programming languages) See modular arithmetic for an older and related convention applied in number theory.

1 Remainder calculation for the modulo operation
2 Common pitfalls
3 Modulo operation expression
4 Performance issues
5 See also
6 Notes
7 References

Remainder calculation for the modulo operation

Integer modulo operators in various programming languages
Language	Operator	Result has the same sign as
ActionScript	`%`	Dividend
Ada	`mod`	Divisor
Ada	`rem`	Dividend
ASP	`Mod`	Not defined
ALGOL-68	`%×`	Always positive
AMPL	`mod`	Dividend
AppleScript	`mod`	Dividend
BASIC	`Mod`	Not defined
bc	`%`	Dividend
bash	`%`	Dividend
C (ISO 1990)	`%`	Implementation defined
C (ISO 1999)	`%`	Dividend
C++ (ISO 1998)	`%`	Implementation defined^[1]
C++ (ISO 2011)	`%`	Dividend
C#	`%`	Dividend
CLARION	`%`	Dividend
Clojure	`mod`	Divisor
ColdFusion	`%`	Dividend
Common Lisp	`mod`	Divisor
Common Lisp	`rem`	Dividend
D	`%`	Dividend^[2]
Eiffel	`\\`	Dividend
Erlang	`rem`	Dividend
Euphoria	`mod`	Divisor
Euphoria	`remainder`	Dividend
FileMaker	`Mod`	Divisor
Fortran	`mod`	Dividend
Fortran	`modulo`	Divisor
GML (Game Maker)	`mod`	Dividend
Go	`%`	Dividend
Haskell	`mod`	Divisor
Haskell	`rem`	Dividend
J	`\|~`	Divisor
Java	`%`	Dividend
JavaScript	`%`	Dividend
Just Basic	`MOD`	Dividend
Lua 5	`%`	Divisor
Lua 4	`mod(x,y)`	Divisor
Liberty Basic	`MOD`	Dividend
MathCad	`mod(x,y)`	Divisor
Maple (software)	`e mod m`	Divisor
Mathematica	`Mod`	Divisor
Microsoft Excel	`=MOD()`	Divisor
Minitab	`MOD`	Divisor
MATLAB	`mod`	Divisor
MATLAB	`rem`	Dividend
Oberon	`MOD`	Divisor
Objective Caml	`mod`	Dividend
Occam	`\`	Dividend
Pascal (Delphi)	`mod`	Dividend
Pascal (ISO-7185 and ISO-10206)	`mod`	Always positive
Perl	`%`	Divisor^[1]
PHP	`%`	Dividend
PIC Basic Pro	`\\`	Dividend
PL/I	`mod`	Divisor (ANSI PL/I)
PowerBuilder	`mod(x,y)`	?
PowerShell	`%`	Dividend
Progress	`modulo`	Dividend
Prolog (ISO 1995)	`mod`	Divisor
Prolog (ISO 1995)	`rem`	Dividend
Python	`%`	Divisor
RealBasic	`MOD`	Dividend
R	`%%`	Divisor
RPG	`%REM`	Dividend
Ruby	`%, modulus()`	Divisor
Ruby	`remainder()`	Dividend
Scheme	`modulo`	Divisor
Scheme	`remainder`	Dividend
Scheme R⁶RS	`mod`	Always positive^[3]
Scheme R⁶RS	`mod0`	Closest to zero^[3]
SenseTalk	`modulo`	Divisor
SenseTalk	`rem`	Dividend
Smalltalk	`\\`	Divisor
SQL (SQL:1999)	`mod(x,y)`	Dividend
Standard ML	`mod`	Divisor
Standard ML	`Int.rem`	Dividend
Stata	`mod(x,y)`	Always positive
Tcl	`%`	Divisor
Torque Game Engine	`%`	Dividend
Turing	`mod`	Divisor
Verilog (2001)	`%`	Dividend
VHDL	`mod`	Divisor
VHDL	`rem`	Dividend
Visual Basic	`Mod`	Dividend
x86 Assembly	`IDIV`	Dividend

Floating-point modulo operators in various programming languages
Language	Operator	Result has the same sign as
C (ISO 1990)	`fmod`	?
C (ISO 1999)	`fmod`	Dividend
C (ISO 1999)	`remainder`	Closest to zero
C++ (ISO 1998)	`std::fmod`	?
C++ (ISO 2011)	`std::fmod`	Dividend
C++ (ISO 2011)	`std::remainder`	Closest to zero
C#	`%`	Dividend
Common Lisp	`mod`	Divisor
Common Lisp	`rem`	Dividend
D	`%`	?
Fortran	`mod`	Dividend
Fortran	`modulo`	Divisor
Go	`math.Fmod`	Dividend
Haskell (GHC)	`Data.Fixed.mod'`	Divisor
Java	`%`	Dividend
JavaScript	`%`	Dividend
Objective Caml	`mod_float`	Dividend
Perl	`POSIX::fmod`	Dividend
PHP	`fmod`	Dividend
Python	`%`	Divisor
Python	`math.fmod`	Dividend
Ruby	`%, modulus()`	Divisor
Ruby	`remainder()`	Dividend
Scheme R⁶RS	`flmod`	Always positive
Scheme R⁶RS	`flmod0`	Closest to zero
Standard ML	`Real.rem`	Dividend

There are various ways of defining a remainder, and computers and calculators have various ways of storing and representing numbers, so what exactly constitutes the result of a modulo operation depends on the programming language and/or the underlying hardware.

In nearly all computing systems, the quotient $q$ and the remainder $r$ satisfy

$q \in \mathbb{Z}$

$a = n \times q %2B r\,$

$\left| r \right| < \left| n \right|.$

This means, that if the remainder is nonzero, there are two possible choices for the remainder, one negative and the other positive, and there are also two possible choices for the quotient. Usually, in number theory, the positive remainder is always chosen, but programming languages choose depending on the language and the signs of a and n.^[2] However, Pascal and Algol68 give a positive remainder (or 0) even for negative divisors, and some programming languages, such as C89, don't even define a result if either of n or a is negative. See the table for details. a modulo 0 is undefined in the majority of systems, although some do define it to be a.

Many implementations use truncated division where the quotient is defined by truncation q = trunc(a/n), in other words it is the first integer in the direction of 0 from the exact rational quotient, and the remainder by r=a − n q. Informally speaking the quotient is "rounded towards zero", and the remainder therefore has the same sign as the dividend.

Knuth^[4] described floored division where the quotient is defined by the floor function q=floor(a/n) and the remainder r is

$r = a - nq = a - n \left\lfloor {a \over n} \right\rfloor.$

Here the quotient is always rounded downwards (even if it is already negative) and the remainder has the same sign as the divisor.

Raymond T. Boute^[5] introduces the Euclidean definition, which is the one in which the remainder is always positive or 0, and is therefore consistent with the division algorithm. This definition is marked as "Always positive" in the table. Let q be the integer quotient of a and n, then:

$q \in \mathbb{Z}$

$a = n \times q %2B r\,$

$0 \leq r < |n|.$

Two corollaries are that

$n > 0 \Rightarrow q = \left\lfloor \frac{a}{n} \right\rfloor$

$n < 0 \Rightarrow q = \left\lceil \frac{a}{n} \right\rceil,$

or, equivalently,

$q = \sgn(n) \left\lfloor \frac{a}{\left|n\right|} \right\rfloor.$

As described by Leijen,^[6]

Boute argues that Euclidean division is superior to the other ones in terms of regularity and useful mathematical properties, although floored division, promoted by Knuth, is also a good definition. Despite its widespread use, truncated division is shown to be inferior to the other definitions.

Common Lisp also defines round- and ceiling-division where the quotient is given by $q =round(a / n)$ , $q=ceil(a / n)$ . IEEE 754 defines a remainder function where the quotient is $a / n$ rounded according to the round to nearest convention.

Common pitfalls

When the result of a modulo operation has the sign of the dividend, it can sometimes lead to surprising mistakes:

For example, to test whether an integer is odd, one might be inclined to test whether the remainder by 2 is equal to 1:

bool is_odd(int n) {
    return n % 2 == 1;
}

But in a language where modulo has the sign of the dividend, that is incorrect, because when n (the dividend) is negative and odd, n % 2 returns -1, and the function returns false.

One correct alternative is to test that it is not 0 (because remainder 0 is the same regardless of the signs):

bool is_odd(int n) {
    return n % 2 != 0;
}

Modulo operation expression

Some calculators have a mod() function button, and many programming languages have a mod() function or similar, expressed as mod(a, n), for example. Some also support expressions that use "%", "mod", or "Mod" as a modulo or remainder operator, such as

a % n

a mod n

or equivalent, for environments lacking a mod() function

a - (n * int(a/n)).

Performance issues

Modulo operations might be implemented such that a division with a remainder is calculated each time. For special cases, there are faster alternatives on some hardware. For example, the modulo of powers of 2 can alternatively be expressed as a bitwise AND operation:

x % 2ⁿ == x & (2ⁿ - 1).

Examples (assuming x is a positive integer):

x % 2 == x & 1

x % 4 == x & 3

x % 8 == x & 7.

In devices and software that implement bitwise operations more efficiently than modulo, these alternative forms can result in faster calculations.

Optimizing C compilers generally recognize expressions of the form expression % constant where constant is a power of two and automatically implement them as expression & (constant-1). This can allow the programmer to write clearer code without compromising performance. (Note: This will not work for the languages whose modulo have the sign of the dividend (including C), because if the dividend is negative, the modulo will be negative; however, expression & (constant-1) will always produce a positive result. So special treatment has to be made when the dividend is negative.)

In some compilers, the modulo operation is implemented as mod(a, n) = a - n * floor(a / n). For example, mod(7, 3) = 7 - 3 * floor(7 / 3) = 7 - 3 * floor(2.33) = 7 - 3 * 2 = 7 - 6 = 1.

Notes

^ Perl usually uses arithmetic modulo operator that is machine-independent. See the Perl documentation for exceptions and examples.
^ Mathematically, these two choices are but two of the infinite number of choices available for the inequality satisfied by a remainder.

References

^ ISO/IEC 14882:2003 : Programming languages -- C++. 5.6.4: ISO, IEC. 2003 . "the binary % operator yields the remainder from the division of the first expression by the second. .... If both operands are nonnegative then the remainder is nonnegative; if not, the sign of the remainder is implementation-defined".
^ "Expressions". D Programming Language 2.0. Digital Mars. http://www.digitalmars.com/d/2.0/expression.html#MulExpression. Retrieved 29 July 2010.
^ ^a ^b http://www.r6rs.org/final/html/r6rs/r6rs-Z-H-14.html#node_sec_11.7.3.1
^ Knuth, Donald. E. (1972). The Art of Computer Programming. Addison-Wesley.
^ Boute, Raymond T. (April 1992). "The Euclidean definition of the functions div and mod". ACM Transactions on Programming Languages and Systems (TOPLAS) (ACM Press (New York, NY, USA)) 14 (2): 127–144. doi:10.1145/128861.128862. http://portal.acm.org/citation.cfm?id=128862&coll=portal&dl=ACM.
^ Leijen, Daan (December 3, 2001). "Division and Modulus for Computer Scientists" (PDF). http://www.cs.uu.nl/~daan/download/papers/divmodnote.pdf. Retrieved 2006-08-27.